As was the case over seven decades ago in the early days of digital computing – when the switch at the heart of the system was a vacuum tube, not even a transistor – some of the smartest mathematicians and information theorists today are driving the development of quantum computers, trying to figure out the best physical components to use to run complex algorithms.
There is no consensus on what, precisely, a quantum computer is or isn’t, but what most will agree on is that a different approach is needed to solve some of the most intractable computing problems.
It may seem odd to have a detailed discussion about several different types of quantum computers at a supercomputing conference, but it actually makes sense for Google, which is a proud owner of one of the first quantum computers made by D-Wave, and researchers from the Delft University of Technology and Stanford University to have talked about the challenges of designing and building quantum computers to tackle algorithms that are simply not practical on modern digital systems, no matter how many exaflops they may have.
The other reason that it makes sense to talk about quantum computers at ISC 2015, which was hosted in Frankfurt, Germany last week, is something that may not be obvious to people, and it certainly was not to us. A quantum computer could end up being just another kind of accelerator for a massively parallel digital supercomputer, and even if the architectures don’t pan out that way, a quantum machine will require supercomputers of enormous scale to assist with its computations.
The joke going around ISC 2015 was that no one really understands what quantum computing is and isn’t, and it was so refreshing to see that in the very first slide of the first presentation, Yoshi Yamamoto, a professor at Stanford University and a fellow at NTT in Japan, showed even he was unsure of the nature of the quantum effects used to do calculations in the D-Wave machine employed by Google in its research in conjunction with NASA Ames. Take a look at the three different quantum architectures that were discussed:
Speaking very generally, quantum computers are able to store data not as the usual binary 1 and 0 states that we are used to with digital machines, but in a much more fuzzy data type called a qubit, short for quantum bit, that can store data as a 1, a 0, or a level of quantum superposition of possible states. As the number of qubits grows, the number of possible states that they can hold grows. The trick, if we understand this correctly, is to take a complex problem that is essentially a mathematical landscape in multiple dimensions, and punch through the peaks of that landscape to find the absolute minimum valleys or absolute maximum peaks that solve for a particular condition in an algorithm when the qubits collapse to either a 0 or a 1. (Oh, we so realize that is an oversimplification, and not necessarily a good one.)
One tricky bit about quantum states, as we all know from Schroedinger’s cat, is that if you observe a quantum particle or a pair that are linked using the “spooky action at a distance” effect called quantum entanglement, you will collapse its state; in the case of a quantum computer, the spin of a particle that respresent the qubit will go one way or the other, becoming either a 1 or 0, and perhaps before you have enlisted it in a calculation. So a machine based on quantum computing, using spin to store data and entanglement to let it be observed, has to be kept very close to absolute zero temperatures and, somewhat annoyingly, has to have quantum error correction techniques that could require as many as 10,000 additional qubits for every one used in the calculation.
This is a lot worse than the degradation in flash memory cells. (You were supposed to laugh there.)
The specs of the D-Wave machine are given in the center column, using a technique called quantum annealing, which is the subject of some controversy with regards to whether or not it is a true quantum computer. At some level, if the machine can solve a particular hard problem, the distinction will not matter so much and perhaps, given the nature of the mathematical problems at hand, perhaps a better name for such devices would be topological computing or topographical computing. The third column in the chart above represents the coherent Ising machine technique that Yamamoto and his team have come up with, which uses quantum effects of coherent light operating at room temperature to store data and perform calculations, specifically a class of very tough problems called NP Hard and using a mathematical technique called Max-Cut.
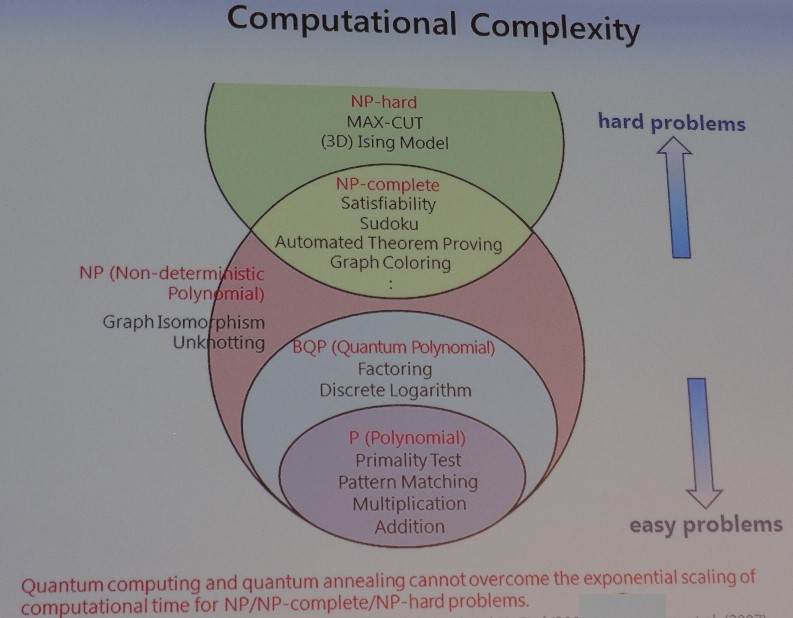
As the chart above shows, there is a range of computational complexity in the nature of computing, quantum or digital.
According to Yamamoto, a set of problems based on what are called combinatorial optimizations can potentially be solved better by a quantum computer than by a digital system. Some examples of combinatorial optimization problems include protein folding, frequency distribution in wireless communication, microprocessor design, page ranking in social networks, and various machine learning algorithms. No direct quantum algorithms have been found for these tough problems, and that means, as Yamamoto put it, as the problem size increases, the computational time to do those calculations scales exponentially.
But there is a way to map these combinatorial optimization problems to what is called the Ising model, which was created almost a century ago to model the spin states of ferromagnetic materials in quantum mechanics. Once that mapping is done, the Ising model can be loaded into qubits in a coherent Ising machine and solved.
Interestingly, Yamamoto says that coherent Ising machines have an advantage over the other architectures because he believes that quantum computing and quantum annealing machines will not be able to escape the exponential scaling issue for hard problems. (Neither of his peers on the panel – Vadim Smelyanskiy, the Google scholar working on quantum computing for the search engine giant, and Lieven Vandersypen, of Delft University of Technology – confirmed or denied this assertion.)
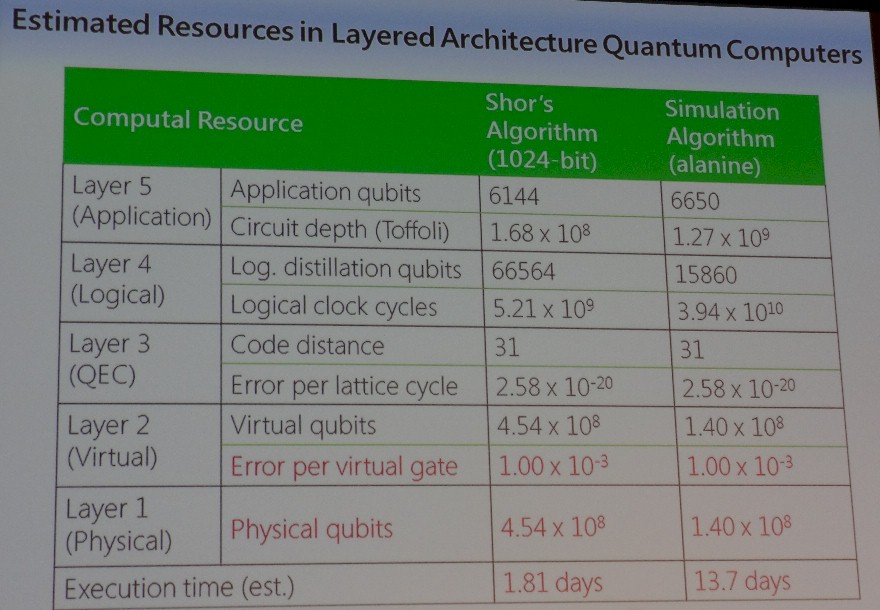
To help us all understand the scale of the architecture of possible future quantum machines, Yamamoto put together this chart, showing the amount of quantum iron it would take to do a factorization problem using Shor’s algorithm, which got quantum computing going, and also showed what size machine would be needed to simulate the folding of an alanine molecule.
In his presentation, Smelyanskiy did not get into the architecture of the 128-qubit D-Wave Two machine installed at Google, but described the mathematics behind the quantum annealing technique it uses. (The math is way over our heads, and was very likely out of reach for others at ISC 2015, too.) What Smelyanskiy did say is that Google has run a number of algorithms, including what is called a weak-strong cluster problem, on classical machines as well as on the D-Wave Two, and as the temperature of the device increases, quantum tunneling kicks in and helps better find the minimums in an algorithm that is represented by a 3D topography.
To get a sense of how a larger quantum computer might perform, Google extrapolated how its D-Wave machine might do with a larger number of qubits to play with:
As you can see, the speedup is significant even as the problem set size grows. But Smelyanskiy wanted to emphasize one important thing, and that this is a very simple alternative to the kind of machine that Yamamoto was talking about to build a circuit model machine that would solve any problem. “If we wanted to build a circuit model, we did a very careful analysis and it would require for similar problems on the order of 1 billion qubits to build, and that is probably something that is not going to happen any time soon, say the next ten years.”
Smelyanskiy said that Google has been working very hard to find applications for its D-Wave Two machines with the NASA Ames team, and thus far the most promising application will be in the machine learning area. (Google will be publishing papers on this sometime soon.)
At Delft University of Technology, Vandersypen expects a very long time horizon for the development of quantum computers, and his team is focused on building a circuit model quantum computer.
“Despite the steep requirements for doing so, we are not deterred,” said Vandersypen. “We are realistic, though.”
“The first use will be for simulating material, molecules, and physical systems that are intrinsically governed by quantum behavior, where many particles interact and where classical supercomputers require exponential resources to simulate and predict their behavior,” explained Vandersypen. “Since a quantum computer is built from the same quantum elements, in a sense, as these quantum systems we wish to understand, it maps very well onto such problems and can solve them efficiently.”
Code breaking and factoring are also obvious applications, too. Solving linear equations that can be applied to machine learning, search engine ranking, and other kinds of data analytics are also possible use cases for a quantum machine.
But we have a long way to go, said Vandersypen.
“What we are after, in the end, is a machine with many millions of qubits – say 100 million qubits – and where we are now with this circuit model, where we really need to control, very precisely and accurately, every qubit by itself with its mess of quantum entangled states, is at the level of 5 to 10 quantum bits. So it is still very far way.”
The interesting bit for the supercomputer enthusiasts in the room was Vandersypen’s reminder that a quantum computer will not stand in isolation, but will require monstrous digital computing capacity. (You can think of the supercomputer as a coprocessor for the quantum computer, or the other way around, we presume.)
“In particular, to do the error correction, what is necessary is to take the quantum bits and repeatedly do measurements on a subset of the quantum bits, and those measurements will contain information on where errors have occurred. This information is then interpreted by a classical computer, and based on that interpretation, signals are sent back to the quantum bits to correct the errors as they happen. The mental picture of what people often have of a quantum computer is a machine that is basically removing entropy all the time, and once in a while it is also take a step forward in a computation. So you need extra signals that steer the computation in the right way.”
With 10 million qubits, the data coming out of the quantum computer will easily be on the order of several terabits per second, Vandersypen pointed out. As the number of qubits scales, so will the bandwidth and processing demands on its supercomputer coprocessor.
To accelerate the development of a quantum computing machine like Delft and others are trying to build will require innovations in both hardware and software. It is not possible, for instance, to take the waveform generators, microwave vector source, RF signal source, FPGAs, and cryo-amplifiers that make up a qubit in the Delft labs and stack them up a million or a billion times in a datacenter. The pinout for a quantum computer is going to be large, too, since every qubit has to be wired to the outside world to reach that supercomputer; in a CPU, there are billions of transistors on a die, but only dozens to hundreds of pins.
For quantum computers using the circuit model, Vandersypen says that 5 to 10 qubits is the state of the art, and researchers are aiming for 50 to 100 qubits within the next five years or so. “That is simply not fast enough,” he says. “We really have higher ambitions and are thinking about ways to push up that slope by partnering with engineers and with industry to more rapidly achieve the really large number of quantum bits that can actually solve relevant problems.”
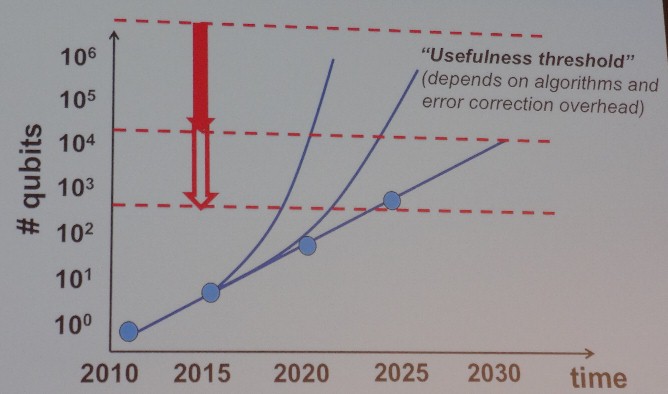
The other thing that Vandersypen wants to do is push down the error correction needed for qubits to run specific algorithms, also accelerating the time when quantum computers become useful. Add these efforts together, and a practical and powerful quantum computer could become available sometime between 2020 and 2025, instead of between 2040 and 2050, as the chart above shows.
So when will we see a quantum computer, of any kind, that can solve at least one hard problem that we care about?
“We can build a 10,000 spin quantum Ising machine in four years’ time, and the particular problems here with Max-Cut are, at least with the computational time, probably four orders of magnitude faster than the best approach possible by GPUs,” said Yamamoto. “Then the question becomes what is the application of Max-Cut can be applied to. We don’t have a focus on any specific target right now, but some sort of reasonable combinatorial optimization problems should be solved by this machine.”
When asked to put a more precise number on it, Vandersypen had this to say: “For the circuit model of quantum computing, the one based on quantum error correction codes and so forth, I think that in the next five years there is no realistic prospect of solving relevant problems unless there is a breakthrough in solving a few qubit algorithms. We are hopeful that on a ten to fifteen year timescale this is going to be possible, and even that is ambitious.”
Smelyanskiy changed the nature of the question away from time and towards money, which was an unexpected shift. Here is what he said:
“We did an analysis at Google recently in what it would take to implement a Grover’s algorithm for extremely hard problems where classical algorithms fail beyond 40 or 50 bits and with 70 bits you would not be able to do it. Grover’s algorithm is a search algorithm that provides a quadratic speedup for extremely hard problems; if you have 2n steps to find the solution on structured search, you would need only n/2 steps to find a solution with that algorithm on a quantum machine. For a problem of size 60, you would need about 3.5 billion qubits and it would take about three hours with a speed up over a single CPU of over 1.4 million times. For the problem of size 70, the speedup would be 34 million and you would need only a little bit more qubits at 5.9 billion. If it is about $1 per qubit, and you spend another $500 million to bid down the price, roughly with a $2 billion investment you would be able to build a decent supercomputer with several millions of CPUs.”
This is much more of a grand challenge than IBM’s BlueGene effort started 15 years ago for a cool $1 billion. The question is, who is going to pay for this?









Be the first to comment