Transactional Memory Comes To The Storage Hierarchy

These are exciting times for the memory hierarchy in systems. New kinds of DRAM and non-volatile memories are becoming available to system architects to enhance the performance and responsiveness of the applications that run upon them. One emerging technology that is gradually being adopted on a couple of server-class processors is transactional memory, which is an ingenious use of concepts already known to both processor cache and database designers for main memory.

At the highest level, what transactional memory is a means of speeding up shared data processing by avoiding the overhead of applying and then freeing locks over the data that is being acted upon. And in today’s processing world, where compute performance is coming largely from parallel processing, such a function will become increasingly useful.

But what is transactional memory really? To explain, we start with the notion of a transaction, and in this case, we mean a database transaction.

A database is just a place to save information, but it is also a bit of a science in its own right. One of the concepts key to database management is that of a transaction, which is a unit of work and which produces all of its results successfully or it produces nothing. Those are the only two choices. A transaction ensures that when you are transferring money from one bank account to another, either the money removed from one shows up on another or no money is removed from the source account at all. In database parlance, this is the atomicity part of the notion of ACID properties for databases: Atomicity, Consistency, Isolation, and Durability. Transactional memory supports a directly related, but slightly different, concept.

More subtle and nuanced is ACID’s concept of isolation. At its most simple level, isolation says that until a transaction – we’ll call it T1 – has successfully reached its end, no other transaction – T2 – executing concurrently is allowed to see any partial results produced by T1. T1’s results together become visible to other transactions like T2 at the end of T1 when T1 commits all of its results. Other transactions see either the entire result of the transaction T1 or they see nothing from T1; they don’t get to see partial results along the way. Although transactions like T2 can be executed during the same period of time as T1, isolation is a bit like ensuring that only one transaction is executing at a time. This, too, is a basic concept supported by transactional memory.

Transaction isolation is nuanced in that a program using a database can trade off performance – in the sense of allowing multiple transactions to concurrently execute while touching the same data – versus the level of control over seeing changed data.

For example, isolation levels called:

• Read Committed ensures that a transaction T2 will not be allowed to see any results from a transaction T1 until T1 is done and has committed all of its changes.
• Repeatable Reads is stronger in its control and goes on and says that if transaction T1 reads some data at any time during T1, T2 will not be able to change that data until T1 ends. The intent is to allow T1 to again re-read the same data and see again what it had previously read. You can have this level of isolation, but this typically means that you execute slower or less in parallel.

The essence of this is that, given that multiple transactions, accessing the same data in some way, and desiring to be executing at the same time, the isolation level dictates what each gets to access when. This, again, is part of transactional memory.

For each of these attributes of transactional memory, we’ll be looking at how it is supported shortly. First, though, let’s take a look at what it is that transactional memory is buying us. I mean, if a Transaction can execute just fine as is, why would be need transactional memory?

Of Locks (Or Not)

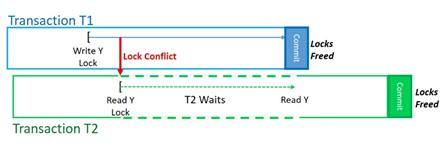
We said that a transaction T1’s results – and there might be a lot of them – are not visible to other transactions until T1 had committed these results. OK, so how? What keeps the changed results invisible? Locking. A lock – a software construct – says “This is mine for the time being. If you want it too, you’ll need to wait around a while until I free up the lock.” There can also be a lot of such locks applied during a transaction to the data of a database. Depending on the transaction’s complexity and Isolation level, even a single transaction T1 can have applied scads of locks within the bounds of T1. Any other transaction that conflicts with T1’s locks may have to wait to access the locked portion of the database. When T1 frees its locks, perhaps many of them, at the end of the transaction, at transaction commit time, only then is the data made visible and the waiting transaction(s) can see T1’s results. Not only is the performance of other transactions impacted, but – perhaps more importantly to transactional memory – it takes time to apply and then free such locks.

Executing a notion of a transaction, and doing it without any such locks, is also one of the attributes of transactional memory.

Before I go on, although the term transactional memory is based on all of the notions of database Transactions outlined here, I need to quickly point out that transactional memory as implemented so far cannot support the complexity of many types of database transactions. You will see why shortly. It can support transactions which are more complex than that of the primitive atomic updates – which we will be looking at next – but not necessarily what some might think of as a rather typical database transaction.

Finishing up here on locks, what locks are generally all about is holding off (i.e. pausing) the execution of an otherwise concurrently executing transaction until the lock conflict goes away. Doing so requires that the transactions apply locks over what is accessed, even if the probability of such conflicts are remote. Again, such locks – and the resulting overhead – are required, even if shared data conflicts are very rare; if it can happen, lock protection is still needed. I mean, would you trust a bank who tells you that they are 99.99 percent sure that they won’t lose your money transfer? If there is even the slightest potential that database isolation and atomicity might be violated, locks are applied and later freed to ensure that the database’s ACID requirements are met.

But suppose that you could ensure atomicity and your expectations on isolation without using locks. Suppose that your transaction – with hardware assistance for performance – could detect that isolation for your transaction was violated or that your transaction would violate the isolation of another. And detecting such, suppose that you knew enough to start over again, this time executing the transaction from beginning to end and still maintaining atomicity and isolation. That detection and informing of the need to restart is also one of the attributes of transactional memory.

Cache And Primitive Atomicity

We’ll be seeing one implementation of transactional memory shortly, but I first want to provide a conceptual building block. We are going to first show how cache is used to support primitive atomicity and doing this without locks.

When I say “primitive atomicity” here, I am referring to being absolutely sure that when multiple processors are concurrently updating a simple primitive variable like a 32-bit integer, each change will be made just as though each had been done at different times on the same processor.

To get the point across, let’s look at what happens if this was not supported. Let’s assume that we have two processors simply adding the number 1 to a 32-bit integer in memory. When done by one processor after the other, the variable will have been advanced by 2. Simple, right? Well, when done at the same time, the result still often appears as plus 2, but occasionally not; occasionally the result ends up being advanced only by 1. Not acceptable. The problem stems from the fact that the variable is not actually incremented in memory. At separate times, the processors

1. Read the 32-bit integer from memory,
2. Increment the 32-bit integer, and then each
3. Stores the updated 32-bit integer back to its location in memory.

If both read the same value, incremented that same value, and both stored the same incremented value, the result would have been an increment by one, not two. You can see this in the following animation using MIT’s Scratch. The 4-byte integer of interest is held within a data block – say 128 bytes in size – which is read into the cache of both processors; the shared integer is read from and then returned to there. Remember you want to see a result as though the operation is first done by one processor and then the other, with the second using the results of the first. In this animation, both processors end up storing the same value, something that can and does happen.

Again, the problem is that your program expected to see that each processor individually had incremented the variable by one, as though done “atomically”. To ensure that, there is specialized support for such “atomic” operations. This special support – which gets requested in software as an “atomic” add – is built on top of the normal functions available in the cache.

Go back to that previous animation and notice what happens with the cache line in processor P1 when P0 initiates its store; it gets invalidated on P1. Similarly, P1’s store invalidates (and copies) the data block in P0. Each store to a data block in the cache always ensures that the old values are not perceivable by other processors. After the store occurs, that newly stored value becomes visible to other processors when they subsequently re-read from that same data block. Said differently, an exclusive (i.e., single-instance) version of that data block must exist on the processor doing the store (and nowhere else). As a result, the data block with our integer is invalidated on P0 when P1 does its store. In effect, P1 had stolen the data block away from P0. Again, this is completely normal operation in a cache-coherent SMP.

Support for “atomicity” is built on this. What we want to have happen is – even though both processors may be reading and incrementing the same value – is that both incremented values actually show up in memory; “atomicity” means that each increment – each read-modify-write – is done as though done one after the other.

In order to support the atomic requirement, the hardware needs to detect that – at the time of the attempt to store an incremented value – that integer variable in the cache still contains the pre-incremented value. That is, whatever value P0 reads from P0’s cached data block before the increment is still there in P0’s cache at the time of the store. Only then can the store associated with our atomic increment be allowed to succeed.

Easy to say, of course, but how does the hardware know that the integer variable had not changed? The processor is not going to read it again. Instead, a processor can know this simply by also knowing that its cache still contains the same data block from which the pre-incremented value had been read. Said differently, a value can be read-modified-written atomically if no other processor had stolen the data block during that time. If processor P0 was guaranteed an exclusive copy of the data block throughout the entire primitive read-modify-write operation, its atomic increment will have succeeded. If not, if P1 had stolen the data block, P0 needs to restart the entire read-modify-write, continuing this until it is true.

You can see in the MIT Scratch animation mentioned above both unsuccessful and successful attempts at atomic updates.

Notice that, if not for P1 stealing and then modifying the data block first read by P0, P0 would have first succeeded in doing an atomic update. But because P0 did not have the original data block, P0’s store failed; it needed to re-read the data block from P1 and the same integer – now modified by P1 – in order for its own atomic update to succeed.

In this simple example, what might appear in a program as a simple increment, in the hardware is actually multiple distinct operations. Somehow, building on normal cache coherency, these multiple operations were able to be perceived by the program as one single atomic operation.

It is this that is the beginning of transactional memory. The “transaction” we just looked at just happens to consist of only a single atomic increment. In the next part of this analysis of transactional memory, we will discuss what happens when you start juggling lots of transactions.