Sometimes, to appreciate a new technology or technique, we have to get into the weeds a bit. As such, this article is somewhat more technical than usual. But the key message that new libraries called ExaFMM and HiCMA gives researchers the ability to operate on billion by billion matrices using machines containing only gigabytes of memory, which gives scientists a rather extraordinary new ability to run on really big data problems.
King Abdullah University of Science and Technology (KAUST) has been enhancing the ecosystem of numerical tools for multi-core and many-core processors. The effort, which is a collaboration between KAUST, the Tokyo Institute of Technology, and Intel, has focused on optimizing two types of scalable hierarchical algorithms for both types of processors: fast multipole methods (FMM) and hierarchically low-rank matrix (or H-matrix) methods for linear algebra. The importance of the KAUST ecosystem contributions can be appreciated by non-HPC scientists as numerical linear algebra is at the root of nearly all applications in engineering, physics, data science, and machine learning. The FMM method has been listed as one of the top ten algorithms of the 20th century.
The end result is HPC scientists now have the ability to solve larger dense linear algebra and FMM related numerical problems than previously possible within a given memory using current highly optimized libraries running on the same hardware, and they can do it faster than is possible for currently feasible problem sizes. The margins of memory compressibility and time reduction depend upon accuracy requirements and are user-tunable, unlike the exact methods they propose to complement.
These methods have been made available in highly optimized libraries bearing the names of ExaFMM and HiCMA, which you can see from those links are made freely available on the GitHub repository. KAUST notes these algorithms have the potential of replacing the today’s “workhorse” kernels in a wide variety of common applications.
In the case of HiCMA for example, think of processing really big billion by billion sized matrices using CPU technology in a mathematically and computationally efficient manner. Represented exactly (in double precision), this problem would occupy 8 EB (the abbreviation for exabytes still does not look normal), but a low rank representation for matrices that commonly arise in spatial statistics or boundary elements, for example, can live in mere gigabytes. Performance can exceed that of highly optimized libraries such as Intel Math Kernel Library (Intel MKL) on large problems because they utilize algorithms that have a rare combination of O(N) arithmetic complexity and high arithmetic intensity (flops/byte). It should be noted, however, that the HiCMA low-rank approximation technique can’t be considered as a general replacement to traditional high performance libraries because it can be applied only to a narrow, yet valuable, subset of the wide range of real computational problems, which can be solved by Intel’s Math Kernel Library software tools.
Putting HiCMA in context, the low-approximation approach augments a subset of the direct methods used by highly optimized libraries such as Intel MKL rather than fixing a flaw or correcting performance or implementation issue. In fact, HiCMA calls various Intel MKL direct methods because they are both fast and accurate.
Domain scientists will appreciate how these freely available libraries can be called from codes in molecular dynamics to benefit drug and material design, quantum chemistry to benefit catalysis and nanoscience, sparse matrix preconditioning that will benefit codes in many areas include structural and fluid dynamics, and provide covariance matrix manipulations to benefit statistics and big data analytics, and more.
Powering A Renaissance In Dense Linear Algebra
Hatem Ltaief, senior research scientist at KAUST and the Intel Parallel Computing Center (Intel PCC) collaborator has been testing the Hierarchical Computations on Manycore Architectures (HiCMA) library on various CPU families. HiCMA provides an approximate yet accurate dense linear algebra package that can operate on really big, billion rows by billion columns matrices. Ltaief states: “The ability to perform matrix operations at this scale represents a renaissance in dense linear algebra.”
The HiCMA effort focused on optimizing the dense linear algebra algorithms to run efficiently across several generations of multi-core processors including Intel Xeon processor families), and also on the latest “Skylake” Xeon SP and many-core “Knights Landing” Xeon Phi processors that can utilize wide vector Intel AVX-512 instructions.
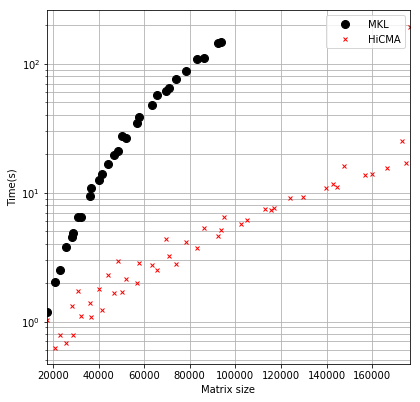
An example set of runs using a Xeon SP is shown below. These results show that, for some problems that can benefit from the low-rank approximation approach, HiCMA provides significantly faster runtimes and smaller memory footprint as the matrix size gets large compared to the memory and runtime behavior of the highly optimized Intel MKL. Note the use of a log scale for runtimes.
HiCMA Optimization
The principal investigators preface their work by observing that numerical linear algebra is at the root of almost all applications in engineering, physics, data science, and machine learning and further, that the HPC community is systematically replacing them with equivalents based on hierarchically low-rank approximations to save on storage and number of arithmetic operations. David Keyes, professor and director of the Extreme Computing Research Center at KAUST and Intel PCC collaborator says, “one should address the curse of dimensionality with the blessing of low-rank.”
Utilizing these equivalents introduces significant memory and instruction operation count savings. The good news from the full KAUST report is that the user can control the numerical accuracy of these equivalents to meet the required numerical accuracy of the application, while significantly outperforming existing dense linear algebra implementations.
Computational Advantages
At its heart, HiCMA uses a hierarchical decomposition of the computation into blocks or tasks that can be executed in parallel. Of course, the decomposition varies depending on the dense linear method being implemented. The following show a representative example for a two-dimensional BEM (Boundary Element Method) using various leaf sizes and a fixed order of interpolation (for example, 2) for the Taylor polynomial expansion. The red diagonal blocks are stored in full rank (dense). Therefore, their rank increases as the maximum leaf size increases.

The key point is that the number of dense (for example, red) blocks is small relative to the sparse blocks so there can be a significant memory savings. Further, an execution graph can be constructed to process the blocks in parallel which (1) exploits the parallelism of the multi- and many-core processor, (2) blocks can be prefetched and mapped into high-performance cache and/or near-memory to increase performance, and (3) vector instructions can be utilized to accelerate the arithmetic operations performed in each block.
The memory savings can be significant and as the first figure shows, can make the difference between being able to perform a computation or not.
To be more specific, a dense matrix of size N that requires N2 storage locations in a traditional array format, while it only requires O(k/nb N2) storage in the HiCMA H-matrix format, where k is the rank of a typical off-diagonal block and nb the tile size, such that 0 < k << nb << N. The KAUST team notes: “In applications for which hierarchically low-rank techniques are of interest, k can be quite small, for example, less than 100, even if N is in the millions – while nb is a critical parameter as it determines the level of concurrency.” The result is a significant memory savings, as well as the performance advantages previously mentioned.
Numerical Accuracy
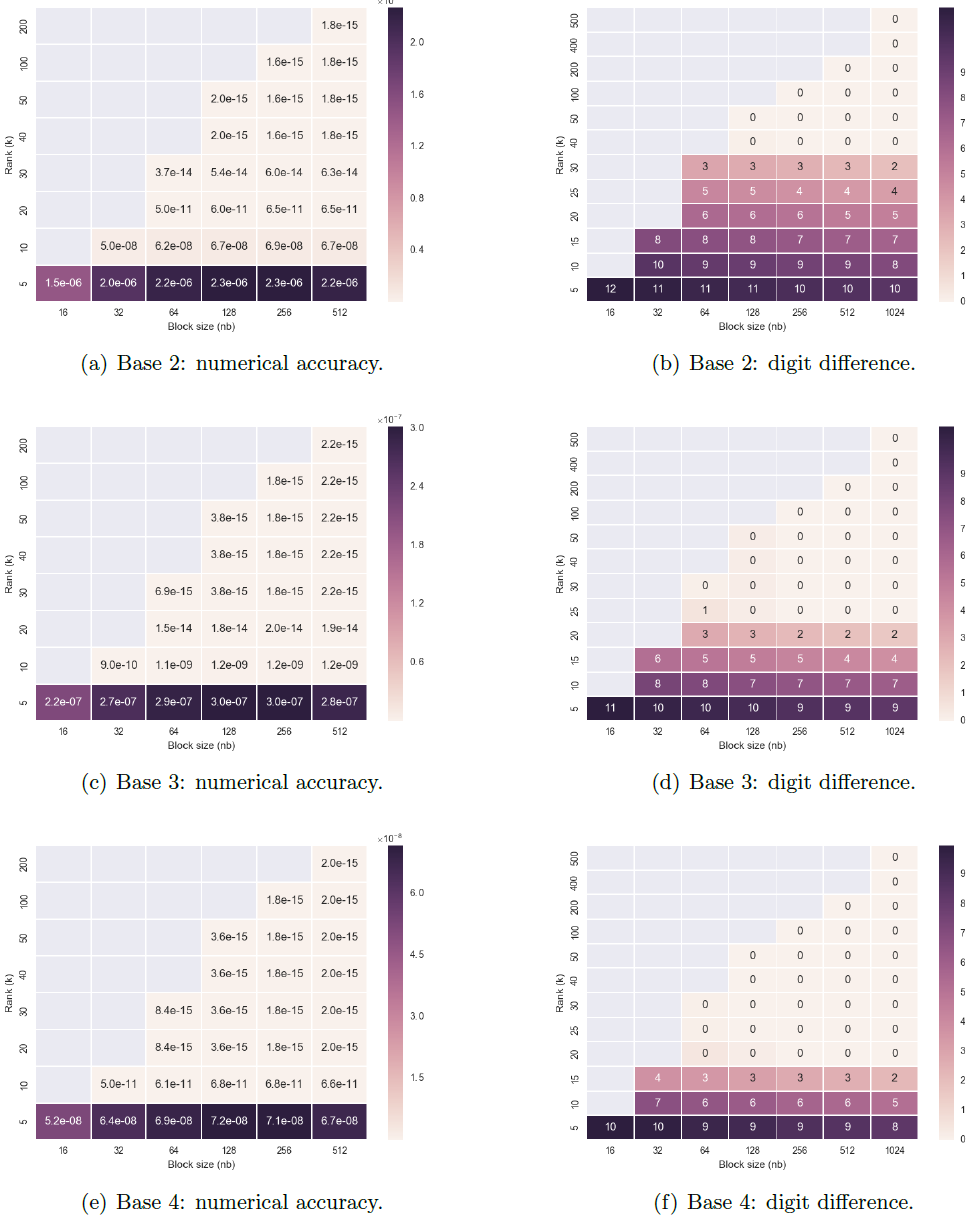
The KAUST team has conducted a wide range of numerical tests using HiCMA and showed that it can deliver accuracy-controlled algebraic result by exploiting advances in solution algorithms and high performance on many-core computer architectures compared to current dense linear algebra libraries such as Intel MKL.
For illustration, we use one of their examples on covariance matrices. These matrices are ubiquitous in computational science and engineering and further they tend to be large, hence the need for HiCMA. The key observation is that, “covariance matrices in which correlation decays with distance are nearly always hierarchically of low-rank.” Off-diagonal low-rank blocks can, for a given accuracy, be replaced with their singular value decompositions, potentially requiring far less storage and far fewer ops to manipulate.
The team uses the following to illustrate the impact of this observation that the decomposition can provide very high accuracy. Note the high precision and digits of accuracy in each cell of the table for a given rank/tile size configuration.
Computational Advantages Of ExaFMM
ExaFMM is a Fast Multipole Method library that intends scale well enough to run on exascale computer systems once they become available. It implements the fast multipole method (FMM) to calculate the long-range force in the n-body problem. This method has more general applicability and can be used to accelerate other problems as well from computational electromagnetics to density functional theory calculations in quantum chemistry.
The data structures of implementation are tree-based and complex, but simply stated, particle interactions are grouped hierarchically so that distant groups of particles interact more sparsely. Hence the characterization of FMM as a hierarchical method.
Rio Yokota notes: “This is an improvement over direct summation, and even over the Fast Fourier Transform, where even remote data points require an amount of communication between them equal to nearby points.” In practice, the data flow of FMM is very efficient and is analogous to a wide area mail delivery system (such as FedX and UPS) in which packages of information are integrated into a hub, transported with high bandwidth, and then parceled out again as needed.
Succinctly, parallelization is achieved by exploiting the freedom to schedule each source-to-target path independently while respecting the FMM execution order within a path. The KAUST team investigated the efficiency of both Cilk and Intel Threading Building Blocks for thread scaling on both multicore and many-core processors, and through the use of MPI both within and across computational nodes. Further, certain phases of the FMM calculation are made in heaven for benefit from the use of the Intel AVX-512 vector instructions.
Numerical Applicability
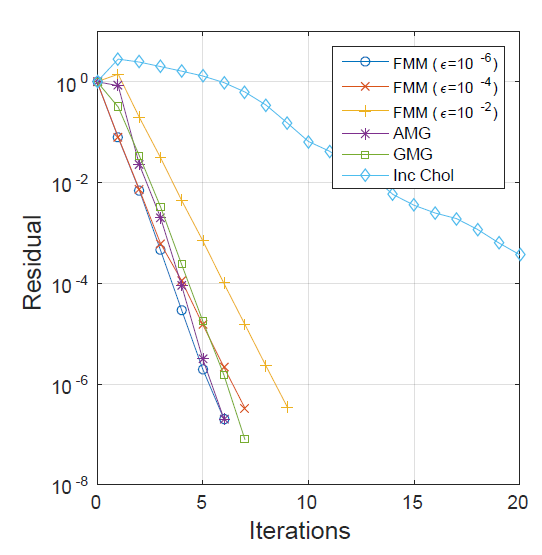
To demonstrate the versatility of ExaFMM, the KAUST team compared the convergence rate of the ExaFMM library when used as a preconditioner against other common preconditioners. For the mathematically inclined, the team preconditioned the classic benchmark linear system from a Laplace equation in a square geometry and looked at the convergence rate.
The results are impressive as can be seen below, as the ExaFMM preconditioner delivered a better convergence rate compared against algebraic multigrid, geometric multigrid, and incomplete Cholesky preconditioners. The ϵ represents the precision of the FMM, where ϵ = 10-6 corresponds to six significant digits of accuracy.
Conclusion
The ability to support very large scale linear algebra, far beyond what can be processed by current highly optimized numerical libraries, opens up new science and engineering applications leading to apparently dense, but data-sparse, problems at scale. Similarly, an exascale capable FMM library (e.g. ExaFMM) will benefit many naturally sparse applications. Thus, the KAUST/Intel PCC collaboration has made a valuable contribution to the numerical tools ecosystem for HPC computing.
Rob Farber is a global technology consultant and author with an extensive background in HPC and in developing machine learning technology that he applies at national labs and commercial organizations. Rob can be reached at info@techenablement.com





Be the first to comment