
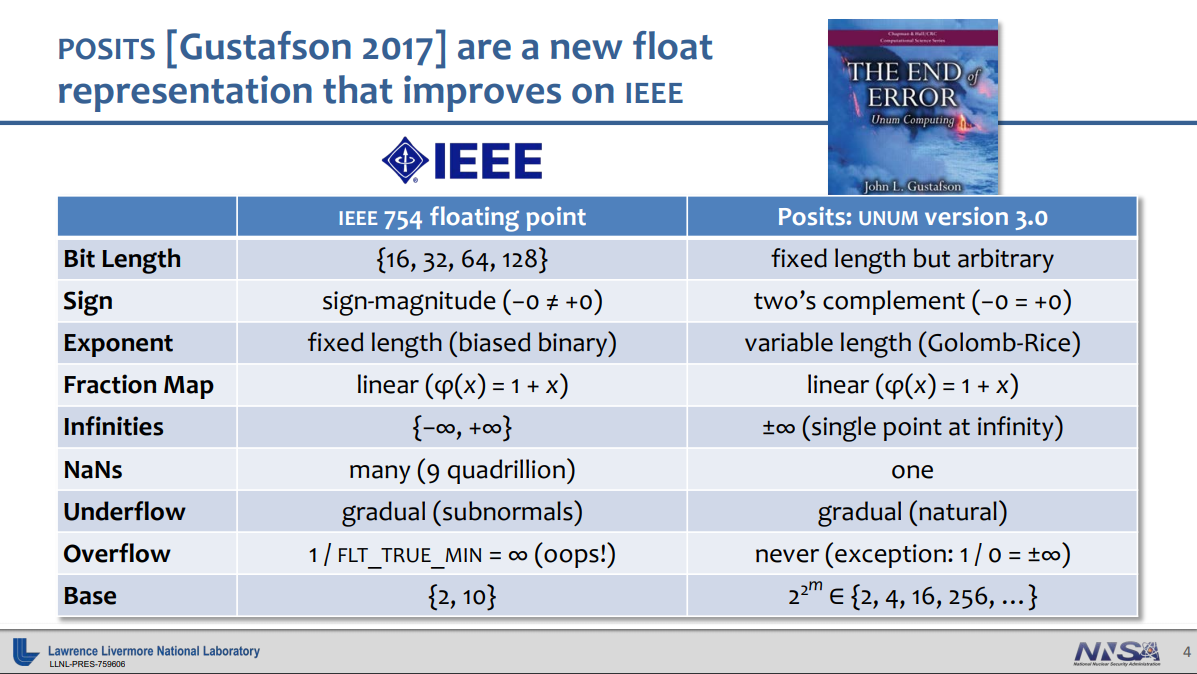
In 1985, the Institute of Electrical and Electronics Engineers (IEEE) established IEEE 754, a standard for floating point formats and arithmetic that would become the model for practically all FP hardware and software for the next 30 years.
While most programmers use floating point indiscriminately anytime they want to do math with real numbers, because of certain limitations in how these numbers are represented, performance and accuracy often leave something to be desired.
That’s resulted in some pretty sharp criticism over the years from computer scientists who are acquainted with these problems, but none more so than John Gustafson, who has been on a one-man crusade to replace floating point with something better. In this case, something better is posits, his third iteration of his “universal numbers” research. Posits, he says, will solve the most pressing problems of IEEE 754, while delivering better performance and accuracy, and doing it with fewer bits. Better yet, he claims the new format is a “drop-in replacement” for standard floats, with no changes needed to an application’s source code.
We caught up with Gustafson at ISC19. For that particular crowd, the supercomputing set, one of the primary advantages of the posits format is that you can get more precision and dynamic range using less bits than IEEE 754 numbers. And not just a few less. Gustafson told us that a 32-bit posit can replace a 64-bit float in almost all cases, which would have profound implications for scientific computing. Cutting the number of bits in half not only reduces the amount of cache, memory and storage to hold these values, but also substantially reduces the bandwidth needed to shuffle these values to and from the processor. It’s the main reason why he thinks posit-based arithmetic would deliver a two-fold to four-fold speedup compared to IEEE floats.
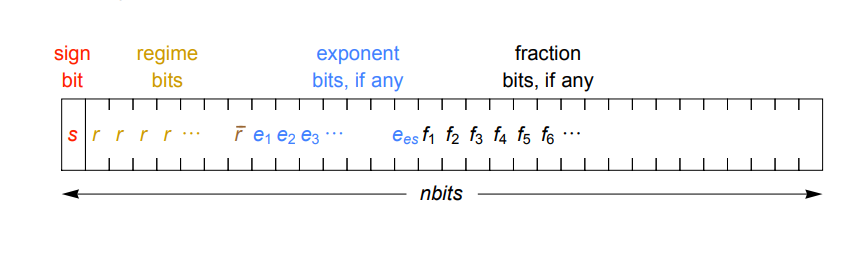
It does this by using a denser representation of real numbers. So instead of the fixed-sized exponent and fixed-sized fraction used in IEEE floating point numbers, posits encode the exponent with a variable number of bits (a combination of regime bits and the exponent bits), such that fewer of them are needed, in most cases. That leaves more bits for the fraction component, thus more precision. The reason for using a dynamic exponent is that it can provide tapered accuracy. That means values with small exponents, which are the ones commonly used, can have more accuracy, while the lesser-used values that are very large and very small have less accuracy. Gustafson’s original 2017 paper on posits provides an in-depth explanation of exactly how this works.
Another important advantage to the format is that unlike conventional floats, posits produce the same bit-wise results on any system, which is something that cannot be guaranteed with the IEEE standard (even the same computation on the same system can product different results for floats). It also does away with rounding errors, overflow and underflow exceptions, subnormal (denormalized) numbers, and the plethora of not-a-number (NaN) values. Additionally, posits avoids the weirdness of 0 and -0 as two distinct values. Instead it uses an integer-like twos complement form to encapsulate the sign, which means that simple bit-wise comparisons are valid.
Associated with posits, is something called a quire, an accumulator mechanism that enables programmers to perform reproducible linear algebra – something not possible with IEEE floats. It supports a generalized fused-multiply add and other fused operations that lets you compute dot products or sums without risking rounding errors or overflows. Tests run at UC Berkeley demonstrated that quire operations are about three to six times quicker than performing the operations serially. According to Gustafson, it enables posits to “punch above their weight class.”
Although the numeric format has only been around for a couple of years, there is already interest in the HPC community to explore their use. At this point, all of this work is experimental, based on anticipated performance on future hardware or by using a tool that emulates posit arithmetic on conventional processors. There are currently no chips in production that implement posits in hardware. More on that in a moment.
One potential application is for the upcoming Square Kilometer Array (SKA), which is considering posits to dramatically reduce the bandwidth and computational load to processes the SKA radio telescope data. The supercomputers that do this need to draw no more than about 10MW and one of the more promising ways they think this can be achieved is to use the denser posit format to slice the anticipated bandwidth of memory (200 PB/sec), I/O (10 TB/sec) and networking (1 TB/sec) in half. Computation would be improved as well.
Another application is for weather and climate forecasting, where a UK-based team has demonstrated that 16-bit posits clearly outperformed standard 16-bit floats and has “great potential for more complex models.” In fact, the 16-bit posit emulation performed on par with the existing 64-bit floating point implementation on this particular model.
Lawrence Livermore National Lab has been evaluating posits and other new number formats, with the idea that they can help reduce data movement in future exascale supercomputers. In some cases, they also found that better answers were generated. For example, posits were able to deliver superior accuracy on physics codes like shock hydrodynamics, and generally outperformed floats on a variety of measures.
Perhaps the largest opportunity for posits is in machine learning, where 16-bits can be used for training and 8-bits for inference. Gustafson said that for training, 32-bit floating point is overkill and in some cases doesn’t even perform as well as the smaller 16-bit posits, explaining that the IEEE 754 standard “wasn’t designed for AI at all.”
Not surprisingly, the AI community has taken note. Facebook’s Jeff Johnson has developed experimental platform with FPGAs using posits that demonstrates better energy efficiency than either IEEE float16 or bfloat16 on machine learning codes. Their plan is to investigate a 16-bit quire-type approach in hardware for training and compare it to the competing formats just mentioned.
Here it’s worth noting that Facebook is working with Intel on its Nervana Neural Network Processor (NNP), or some variation of it, the idea being to accelerate some of the social media giant’s AI workloads. It would not be out of the realm of possibility that a posits format could be used here, although it’s more likely that Intel will stick exclusively to Nervana’s original FlexPoint format. In any case, that’s worth keeping an eye on.
Gustafson knows of at least one AI chip startup that is looking to use posits in their processor design, although he was not at liberty to share which company that was. Kalray, the French firm working with the European Processor Initiative (EPI), has also shown interest in supporting posits in their next-generation Massively Parallel Processor Array (MPPA) accelerator, so the technology may find its way into the EU’s exascale supercomputers.
Gustafson is understandably encouraged by all this and believes this third attempt at his universal numbers may be the one that catches fire. Unlike versions one and two, posits is straightforward to implement in hardware. And given the furious competition in AI processors these days, it may find have found the killer app to make it commercially successful. Other platforms where posits could have a bright future are digital signal processors, GPUs (both for graphics and compute), IoT devices, and edge computing. And, of course, HPC.
If the technology gets commercial traction, Gustafson himself probably won’t be able to capitalize directly on its success. The design, as specified in his initial 10-page standard, is completely open source and freely available to use by any company willing to develop the requisite hardware and software. Which probably explains why companies like IBM, Google, Intel, Micron, Rex Computing, Qualcomm, Fujitsu, and Huawei, among others, are looking at the technology.
Nonetheless, replacing IEEE 754 with something better would be quite the accomplishment, even for someone with Gustafson’s impressive resume. Even before his stints at ClearSpeed, Intel, and AMD, he had been looking at ways to improve scientific computing on modern processors. “I’ve been trying to figure this out for 30 years,” he said.


This sounds a lot more useful than the grade school implementation of “New Math”.
Great article and thank you to Dr. Gustafson for pioneering this brilliant advance. The 3rd iteration looks more than ready for a full roll-out with drums and a fanfare. I would love to donate a composition for it!
LLNL seems to favor ZFP over posits. What then should be implemented across the board? We need a standard, not fragmentation. Maybe new chips should support both, and of course ditch IEEE floats.
ZFP can be applied to posits or floats, LLNL has told me (Peter Lindstrom). They are orthogonal ideas. Lindstrom’s group has a test framework for various number systems that they can use on application codes like Eulerian fluid flow and shock hydrodynamics. They have consistently found that posits achieve the highest accuracy of any number system tested, and IEEE floats achieve the lowest accuracy.
It is true that zfp can be “applied” to posits or floats in the sense that small blocks of numbers in any numerical format can be converted to the zfp format. zfp can be thought of as a number format suitable for small blocks of related numbers. This is somewhat akin to Intel’s FlexPoint format and how SSE/AVX instructions and tensor cores operate atomically on 4-vectors and 4×4 matrices.
Because posits represents scalars and zfp represents vectors/blocks, they serve different purposes. However, for computations involving fields defined on 2D and 3D grids, such as the fluid flow applications John mentioned, zfp generally performs significantly better than both posits and IEEE in terms of accuracy per bit stored. So the statement “posits achieve the highest accuracy of any number system tested” is not quite accurate.
0 and -0 is not a weirdness. it has a meaning in mathematics.. it is used mainly in statistics where it is used to how we are approaching the 0 limit ; x → 0−, x → 0−, or x → ↑0
-0 is used to note that a value 0 has been rounded down to 0 but was not a true 0 before rounding.
While “positive zero” and “negatiive zero” can be used to express limits, the 754 standard says that +0 = –0 in comparison tests. But since 1 / +0 = ∞ and 1 / –0 = –∞, you have a situation where x = y but f(x) ≠ f(y). There is a better way to convey that a number is in the open interval (0, minreal) or (–minreal, 0), or exactly 0, and that allows correct mathematical execution.
Because 0 and –0 have different bit patterns but must test as equal, that mandates a different set of instructions for comparison of real numbers than for integers. Posits can use the exact same comparison instructions as 2’s complement signed integers, saving chip area and simplifying the instruction set.
The early IBM computers of the 1950s used sign-magnitude format for integers, but people soon discovered how wasteful and awkward it is to have two representations of zero, and sign-magnitude format for integers has been obsolete for half a century. It makes addition and subtraction algorithms awkward, with three conditional tests that are not needed for 2’s complement addition and subtraction. It is unfortunate that the IEEE 754 designers reverted to sign-magnitude format in 1985 and did not learn from the experience.
Many of the claims in this article are simply impossible on their face.
“It also does away with rounding errors, overflow and underflow exceptions”. That is simply not possible with any floating-point representation that only uses a finite number of bits. It is also directly contradicted by the earlier statement “the lesser-used values that are very large and very small have less accuracy”.
The claim that IEEE floating point calculations are not reproducible, but posit calculations are, is also self-evident garbage. To be clear, any series of IEEE FP calculations performed sequentially by a single-threaded program will be bitwise reproducible. Of course, most HPC computations these days are done on GPUs or similar parallel processors executing large numbers of threads in parallel, and in that case the order of execution may be randomized, such that the rounding errors are different from run to run. That is, when the order in which terms are combined is allowed to vary, then the rounding errors may vary from run to run. But even on a GPU, the statement that “reproducible linear algebra” is “not possible” is complete bunk. But even if that were the case, how would posits be different? Again, any encoding using a finite number of bits must round off the result of each operation; if the order of combining terms is reproducible, the result will be bit-wise reproducible, and if not, not.
Amen
I agree, but I’ve seen similar claims exaggerating IEEE FP issues before.
As Gilbert Fernandes commented, losing +0 and -0 is not a feature. For arithmetic computation, you don’t need to worry about it, as these values compare equal. There are many cases, however, where these distinct values preserve valuable information that is lost with posits.
My concern is the similar collapse of infinities to a single value (which I suppose should really be called “overflow”, prior claims notwithstanding). If you work with range/interval arithmetic, or with bounding volumes, infinities are real, meaningful values that make operations natural. For example, an interval that contains all real numbers would be min = -∞, max = +∞. An interval that contains no values would be min = +∞, max = -∞. From there, the arithmetic flows without any special cases or special values needed. Adding a value P to the interval is just min ← MIN(min,P), and max ← MAX(max,P). Other operations would be similarly trivial. With posits, the single infinity is useless, and you’d need to resort to special (now reserved) values and conditional branching, a sure performance killer.
This is one example, but a disappointing one, where additional cleverness could have preserved such useful values. (Collapsing all NaNs to a single value, however, is a definite win.)
Unfortunately, the brevity of Feldman’s excellent writeup did not permit a sufficient explanation of what seems like a bombastic and impossible claim, so I understand your reaction. Let me add a few words here, but I do hope you visit the URLs in Feldman’s writeup (to the “posit4” article in particular) for a detailed explanation.
If used the way floats are used, of course posits will produce rounding errors. They will be smaller rounding errors in most cases. When the quire is used, any basic block of plus-minus-times-divide operations can be evaluated without the accumulation of rounding errors, so in effect there is only a single rounding error. This method was pioneered by Ulrich Kulisch back in the 1980s and IBM once offered a product called ACRITH that guaranteed accuracy equivalent to using infinite precision, rounding only at the end, without actually using extended-precision arithmetic like Mathematica and Maple do. It ran slower than normal environments, so it did not succeed commercially.
When posit results are too large in magnitude to represent, they round to maxreal (or –maxreal if negative). The French call this “saturation arithmertic”, and it is strongly recommended by Donald Knuth in the Seminumerical Algorithms book in his Art of Computer Programming series… unfortunately, the IEEE 754 ignored Knuth and rounded to infinity or negative infinity, thereby committing an infinite relative error. Posits commit a large relative error, but not infinite. Similarly, posits do not underflow to zero, but instead get stuck at minreal or –minreal.
Feldman’s sentence “It also does away with rounding errors, overflow, and underflow exceptions” is clearer (and correct) if the word “exceptions” is emphasized in bold or italic. What that means is that exception flags in hardware are not mandated by the Draft Posit Standard. Whereas IEEE 754 mandates the setting of flags when there is rounding, underflow, and overflow, four decades have shown that programmers do not use them. Programming languages do not support them. Instead, the languages have their own POSIX standards for catching and reporting errors. When you try to take the square root of a negative number in C, for example, the compiler takes care of testing for that and for printing an error message. And you can’t view the ‘inexact flag” in any language other than assembler.
As for IEEE floating-point calculations not being reproducible, this is something acknowledged by Kahan, by the latest version (2008) of the IEEE 754 Standard, by Intel in their public presentations on floating point, and in the Wikipedia page on IEEE floating point. The best summary I’ve seen of all the conditions that can lead to this phenomenon is “The pitfalls of verifying floating-point computation” by David Monniaux. There are two major causes: One is that the Standard allows, even encourages, the use of temporary guard bits greater than the nominal size of a number, and compilers continue to exploit the 80-bit register set in all x86 processors to hold 64-bit float results in intermediate calculations even though the vector instructions in x86 processors are strictly 64-bit. When a context switch forces a state save, the 80-bit value is clipped back to its externally-visible 64-bit size, possibly causing overflow/underflow or other errors. The second reason is that while plus-minus-times-divide and square root must be correctly rounded in the standard, transcendental functions in the math library do not need to be. Thus, you cannot expect exp(x) or cos(x) to be bitwise identical from one IEEE-compliant float environment to another.
The Draft Posit Standard, if followed, eliminates both of these problems, and also says that a compiler may not fuse posit operations (for optimization, say) unless explicitly requested by the programmer. It also mandates that all transcendental functions be correctly rounded, and I have found a fast way to achieve this that avoids “The Table-Maker’s Dilemma” so the C algorithms for all of the math library functions will be an Addendum to the Posit Standard when it is completed. I already have most of the 16-bit functions done and some are now visible on a fork of the SoftPosit library on GitLab.
Regarding reproducible linear algebra, dot products done in parallel run into the lack of associativity in floating-point addition, so running LAPACK on a supercomputer will get different results depending on how many processors are used. Posits fix this with the quire, which accumulates the dot product as an exact fixed-point number, and rounds only when converted back to a posit. In a parallel algorithm, partial sums are communicated with quires and not posits, eliminating the problem caused by non-associative addition.
“Then just use a quire with floating-point numbers,” you might say. But there are two reasons that really does not work. For 64-bit floats, the quire is slightly more than 4K bits long, a very large number that is not an integer power of 2 in size. That’s not hardware-friendly. The 64-bit posit quire is exactly 2K bits long, but I’ve found that 64-bit posits are overkill for most linear algebra, and I can use 32-bit posits even on ill-conditioned systems by using the quire to do Dongarra-style residual correction (but unlike Dongarra, I can do the dot products with only a single rounding error). For 32-bit posits, the quire is 512 bits in size, a hardware-friendly number since it’s the width of a typical x86 cache line and also the width of the AVX-512 instruction set data.
I forgot to mention the second reason, in the last paragraph. The IEEE 754 Committee has repeatedly and adamantly rejected the idea of an exact dot product accumulator in the Standard, and in fact they ‘teach against it’ by saying double the working precision for the accumulator is a much more practical way to control rounding error. Even the IEEE 1788 Standard for Interval Arithmetic included the exact dot product for a few months, but then it was taken out by people who did not understand what a powerful tool it is. I don’t blame either committee for being wary of mandating support for a 4,224-bit variable type, which is what you need for perfect dot products of 64-bit IEEE floats.
Thanks for the explanations of what this article was oversimplifying. A couple x86/x87 nitpicks/corrections that don’t contradict your overall points:
The “unpredictable” temporary rounding of 80-bit x87 floats is nailed down at compile time, depending only on optimization options and compile-time stuff. Not context switches or anything else asynchronous that could cause run to run non-determinism for the same binary. Getting deterministic FP from the same *source code* is the hard thing, especially for 32-bit x86 using the x87 FPU. This is why GCC has a -ffloat-store option. But even without that, the IEEE and C/C++ standards allowing contraction of a*b+c into fma(a,b,c) can introduce non-determinism.
Context switches transparently save/restore the full FPU state (using xsave/xrstor or older or newer equivalents), so OSes don’t *asynchronously* round your long doubles to double! And 80-bit fld / fstp have also always been possible, allowing 80-bit long double to be a real type that can survive being stored and reloaded.
—
Compilers targeting x86-64 do use SSE2 or AVX for float/double, so in C terms that’s FLT_EVAL_METHOD = 0, where temporaries have the same width as the source types.
It’s only legacy 32-bit code that sometimes still uses x87 80-bit FP temporaries for float/double. (Most compilers have options to use SSE2 for scalar math even in 32-bit mode). In 64-bit code, only long double ever uses the 80-bit type.
(Some C implementations / ABIs, specifically Windows, define long double to be the same as 64-bit double. Some like MSVC even set the x87 precision-control to round the mantissa to 53 bits after every operation, so 32-bit code using x87 like that is pretty close to FLT_EVAL_METHOD = 1 in C terms. Temporaries still have the exponent range of 80-bit x87, but that doesn’t affect rounding except if values would have been subnormal.)
Again, this is all specific to x86; most other ISAs have FP registers that are like x86’s XMM registers, providing IEEE binary32 and binary64 operations directly.
Related:
https://randomascii.wordpress.com/2012/03/21/intermediate-floating-point-precision/ – including some details on MSVC’s startup code setting the x87 precision-control bits to do more rounding, at the expense of making 80-bit full precision unavailable.
https://stackoverflow.com/questions/27149894/does-any-floating-point-intensive-code-produce-bit-exact-results-in-any-x86-base
https://retrocomputing.stackexchange.com/questions/9751/did-any-compiler-fully-use-intel-x87-80-bit-floating-point/9760#9760 – details on the ability to use the 80-bit x87 type in C, and that it was significantly slower to store/reload, thus it wouldn’t have made sense for compilers to use it transparently when spilling temporaries/locals within a function.
Back in the 16-bit days I ran into a number of problems with floating point data types. Try explaining to your corporate accountant why your program adds a column of figures and is probably $0.01 off from the proper amount, for example.
My first Pascal compiler used Binary Coded Decimal instead of floating point; I wrote a library to use BCD, which was more accurate and usually faster than floating point. And a lot smaller, too.
TRX, back in that day, BCD was faster because it’s simpler to implement on software.
Basically what Jim Conyngham said.
This article really should have been covered by someone who understands IEEE 754.
I have code which (with computer options to enforce IEEE 754 compliance) produces identical results when running single threaded, multithreaded, or even on GPUs.
Kahan was also skeptical of these last I heard, and given all the blatantly wrong things in this article, I don’t think he’s wrong.
Gustafson’s work with variable-precision floating point numbers is interesting, but it does nothing to address a fundamental problem of any base 2^n floating point scheme, which is the mismatch between the base 2^n floating point numbers and the base 10 world in which we live. His posits are still limited-precision values and as such there will still be base-10 fractions which cannot be represented exactly. That inability to represent all base-10 fractions exactly renders posits no better than fixed-precision floating point for many problem domains, most especially for those involving money. I am not saying variable-precision floating point number representation could not be useful – I am saying that this is not a panacea for all the numeric ills of the world.
Food for thought: if base-10 actually mattered, then the financial industry would only buy processors from IBM (because only IBM implements base-10 floating point in hardware), but they don’t. In practice, base-10 only “matters” if you have legacy [COBOL] code that can’t be rewritten to handle base-2 floating point.
Do we really live in a base 10 world? If anything, the “natural” base is e. What is special about fractions with a power of 10 as the denominator? Why do they all need to be represented exactly when you can’t represent 1/3 exactly?
2 years ago, before I started to work on Quantum Compute emulation on conventional hardware, I would not have cared much about modifying the IEEE standard. However. This QC thing *screams* for far, far, far, more precision then the conventional hardware FP registerssupport ATM. Even when it is only to receive and refine results from a real QC rig. Therefore I am fairly sure that a change in the FP approach will come about when large datasets are fed into quantum tubes and very fine ( and very, very long ) answers come about. The 42 thing was overrated anyway 🙂
can’t we just use two bigints for representation of a non-infinite, non-NaN fraction and call it a day?