A New Direction for HPC Math Libraries

HPC luminary Jack Dongarra (University Distinguished Professor University of Tennessee) presented a new direction for math libraries at the International Supercomputing conference (ISC) in Frankfurt Germany in his presentation “Numerical Linear Algebra for Future Extreme-Scale Systems (NLAFET)”.

The Parallel Numerical Linear Algebra for Extreme Scale Systems is a Horizon 2020 FET-HPC project funded by the European Union. It is consortium that consists of four partners: Umeå University (UmU) in Sweden, The University of Manchester (UNIMAN) in United Kingdom, Institute National de Recherche en Informatique et en Automatique (INRIA) in Paris, France, and the Science and Technology Facilities Council (STFC) in United Kingdom. Umeå University is coordinating NLAFET

The aim of the NLAFET project is the development of novel architecture aware algorithms that expose as much parallelism as possible, exploit heterogeneity, avoid communications bottlenecks, respond to escalating fault rates, and help meet emerging power constraints. The result of these efforts, along with other goals such as the evaluation of novel autotuning and scheduling strategies will appear in the NLAFET software library.

Current numerical library design tends to follow an “express the model in a parallel fashion” then later optimize the source code to best run on different machine architectures. Traditionally, this meant that  programmers would focus on expressing the parallelism of loops within their source code to get performance.  This is why Dongarra stated in his presentation, “we abandoned loop level parallelism”.

Instead, the NLAFET project focusses on using Directed Acyclic Graphs (DAGs) that are processed by a runtime system.

The DAG acts as a form of intermediate language that naturally expresses the parallelism and data dependencies of the numerical algorithm without committing to any specific computer architecture. Instead, the decisions about what to parallelize and how data movement is to be choreographed is delayed until a machine-specific runtime interprets the DAG and makes the decisions about how to most efficiently run the computation

In this case, procrastination is a good thing as it makes the runtime and not the algorithm author responsible for making and implementing the many variations needed to run a given architecture. To demonstrate the efficacy of the DAG-based approach, Dongarra presented performance results in his talk for several numerical methods when running on a shared-memory vs. a distributed computer.

Before looking at the performance results, it is important to understand how the DAG naturally represents the computation so the runtime can efficiently perform the calculation on two such disparate architectures.

As can be seen in the schematic below, a DAG consists of a series of tasks (represented by the circles) connected by lines that represent the dependencies.

The NLAFET approach gives each computational node in a distributed system a complete copy of the symbolic DAG.  Different nodes are represented by different background colors in the figure below. This gives the runtime the ability to perform all the work on a single computational device, or to break up the computation across many devices.

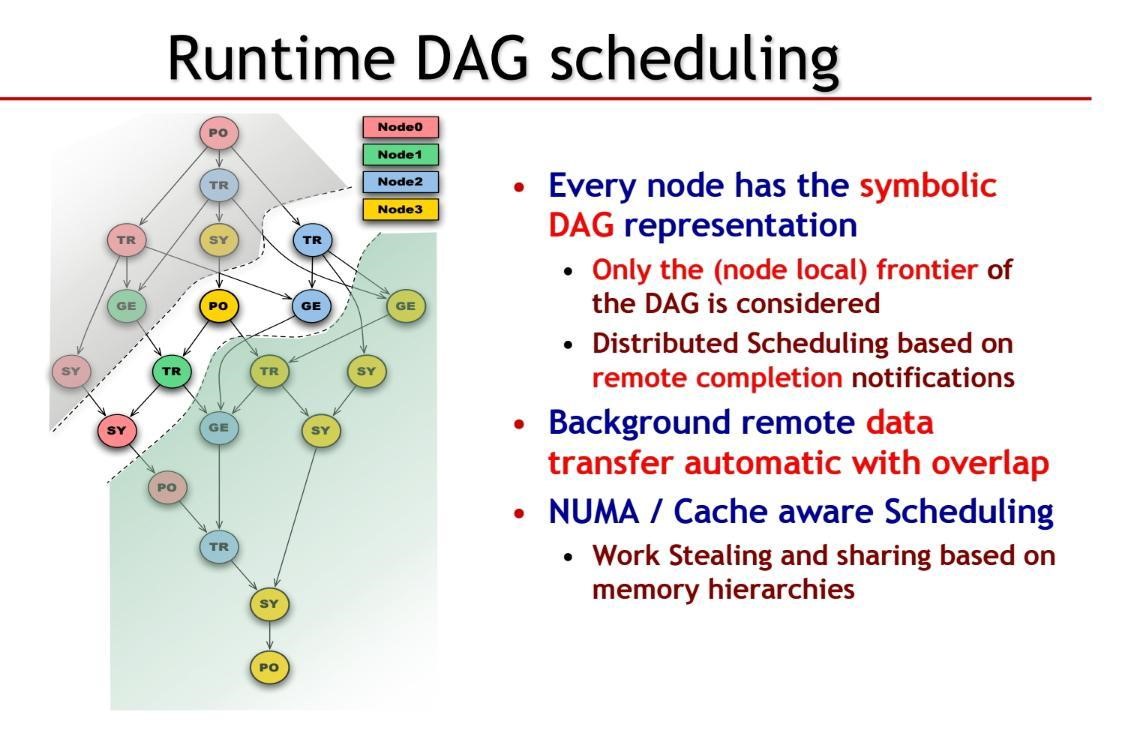
Nodes only process work when all the data dependencies for a task (e.g. all the lines into a circle) are marked completed. This naturally expresses all the parallelism in the algorithm as a single notification can satisfy the dependencies for many tasks which can be ran in parallel according to the machine capabilities. A task can be a computation or a data transfer, so the DAG representation both simply and elegantly expresses the overlapping of computation and data transfers. Distributed scheduling of work across nodes occurs by remote completion notifications, which allows the efficient choreographing of work across all the nodes of a system, be it a small institutional cluster or a leadership class exascale supercomputer.

The data flow based runtime system that processes the DAG can be implemented using a variety of frameworks. The NLAFET effort is investigating the performance characteristics and benefits of OpenMP, StarPU, and PaRSEC. The following task profile shows a 45% improvement in runtime for a Cholesky factorization when using the PaRSEC backend compared to a traditional SIMD/MPI implementation.

Of course, the DAG-based approach is quite general and supports both individual and batched numerical operations. Dongarra summarized the current NLAFET efforts as seen below.

 

In collaboration with the University of Manchester, the NLAFET effort is performing detailed analysis of a number of different dense linear algebra methods using OpenMP 4.5 for shared memory architectures, and StarPU and PaRSEC backends for distributed architectures. Early results shown below indicate the NLAFET approach delivers very competitive performance in both shared memory and distributed environments compared to the well-established LAPACK libraries.

The NLAFET effort represents an excellent next step to architecturally-aware numerical libraries that are scalable and able, via a runtime system, to exploit the performance capabilities of both shared memory and distributed computational systems. We are only seeing first results from this project, but phrasing numerical computations in terms of a DAG is clearly an viable approach for the creation of future, architecture aware libraries.s

Rob Farber is a global technology consultant and author with an extensive background in HPC and advanced computational technology that he applies at national labs and commercial organizations. He can be reached at info@techenablement.com